Sorting
Even an idiot can do it with enough time
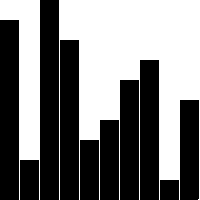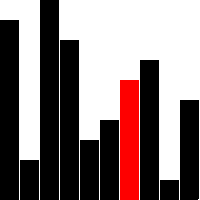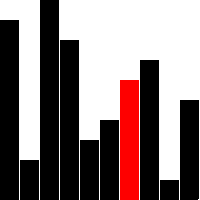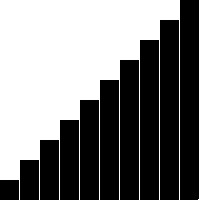
Sorting is one of programmings most popular topics. Given a collection of N objects, how can we arrange these objects such that they are in order? We can put them together by size, color, shape, or any other property. However, to put these objects in order, we need to preform swaps on these items. This is what a sorting algorithm does. Usually, in programing, we sort items using some numeric value. For example, one of the most common uses for sorting is to put integers in ascending order. For the examples below we will sort integer arrays in ascending order. The preconditions is that we are given an integer array filled with integer values and the postconditions are that the array should contain all the same elements in the original array, just in ascending order.
Bubble Sort
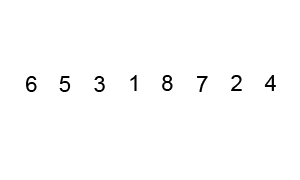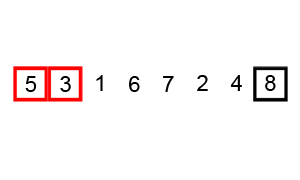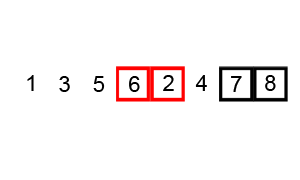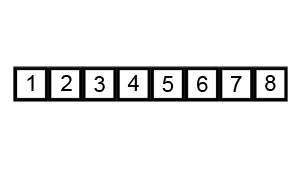
A bubble sort algorithm iterates through the entire array and swaps consecutive items if the item at the larger index is less than the one at the smaller index. At the end of each iteration, the bubble sort checks if the array has been sorted in the correct order. If so, we return the sorted array. Otherwise, we iterate though the array and swap items until the array is sorted in ascending order. The time complexity of this sorting algorithm is O(n^2) as the algorithm requires to iterate through the array at least n times until the array is guaranteed to be sorted (This is n*n=n^2 operations for checking and swapping).
static void bubbleSort(int arr[], int n){ for (int i = 0; i < n - 1; i++) { // loop through array for (int j = 0; j < n - 1; j++) { // loop for swaps if (arr[j] > arr[j + 1]) { // if next object smaller, swap int temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; } } } return -1; // item not found } // a bubble sort where arr is the array to be sorted and n is the size of arrMerge Sort
Unlike other sorts, merge sort works recursively(the method calls itself). A merge sort algorithm first takes in an array and splits in into 2 smaller array of half the size of the original. We take the first half of the original array and put in the first array and we take the remaining of the original array and put it in the second array. We then run a merge sort on both the smaller arrays, until the size of each array passed through the merge sort is of size 1. At this point, we return each subarray and start merging the arrays back together. We take the array containing the first half of the original elements and the array containing the second half and add elements back to the original array in ascending order. The complexity of a merge sort is O(nlogn) as we split the orginal arrays up into halfs, which takes O(logn) time, then we need to rearange everything back together, and since there are n objects, it takes O(n) time, giving O(nlogn) time in total.
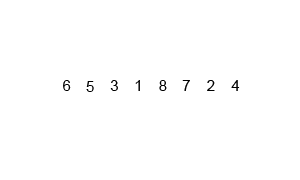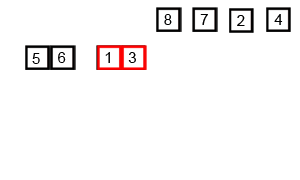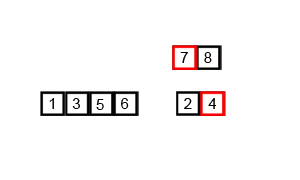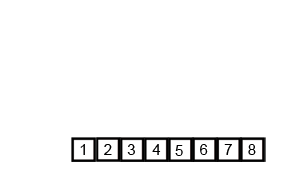
public static void mergeSort (int arr[], int n){ // a merge sort written with a merge util method if(n == 1) return; // arr is the array to be sorted and n is the size of arr int x = n/2; // find size of new array int[] left = new int[x]; // construct new arrays int[] right = new int[n-x]; for(int i = 0; i < x; i++){ // fill arrays left[i] = arr[i]; } for(int i = x; i < n; i++){ right[i-x] = arr[i]; } mergeSort(left, x); // sort arrays mergeSort(right, n-x); merge(arr, right, left, x, n-x); // merge arrays}private static void merge (int a[], int r[], int l[], int left, int right){ int i = 0, j = 0, k = 0; // set indexes for arrays while (i < left && j < right){ // while next index is avalible if (l[i] <= r[j]){ // if left element is less, add to original a[k++] = l[i++]; } else { a[k++] = r[j++]; // otherwise add right element } } while (i < left){ // add remaining elements a[k++] = l[i++]; } while (j < right){ a[k++] = r[j++]; } }