Searching
So you can find things (duh)

In programing, searching algorithms are used to find specific items in arrays or lists. These items are called keys. The array can be of any type or object, as long as there is a valid criteria to search for. An algorithm will return the index of the occurrence of the key in the list or array. There are both fast and slow searching algorithms that can affect the performance of your program. You can also be a searching program! Can you find Waldo on the picture to the left? The precondition of a search should be that the array or list entered consist of unique elements.
Linear Search
A Linear search iterates through each element of a array or list until it finds an element matching the inputted key. It starts at the first element (index 0) and keeps moving up on elements until we reach the last element. If the key if found while iterating through, then we stop and return this index and terminate the program. The postcondition of a linear search is that the element was found, or entire array has been iterated through if the element was not found and -1 is returned in this case. This takes O(n) time where n is the length of the array as we do an operation for each element in the array.
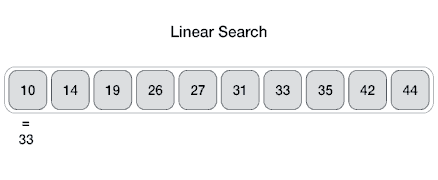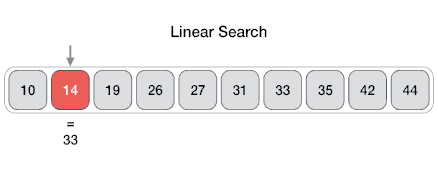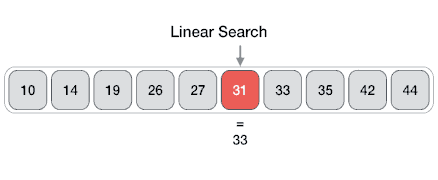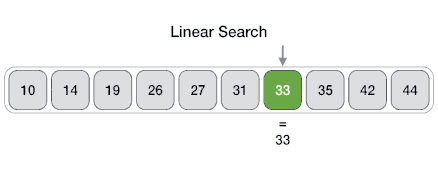
public static int search(int key, int [] arr) { for(int i = 0; i < arr.length; i++) { if(arr[i] == key) { return i; } } return -1;} // a linear search algorithm for a int arrayBinary Search
A binary search algorithm works by cutting an array or list in half until it finds the key. For this strategy to work, the array or list must be sorted in some sort of ascending format (check out sorting). Given the collection is sorted, we check the middle element of the collection and see if it equals the key. If it does, we return the index. If the element in the middle is larger than the key, we rerun the binary search on the lower half of the array as we know the element would have to be there if in the collection. Otherwise, we rerun the binary search on the top half of the collection. We keep doing this until the element is found. A binary search can we written both recursively or iteratively. The postcondition of a binary search is that the element was either found, or we hit a point where the cut of the array has 0 elements, in which -1 is returned. The time complexity of a binary search is O(logn) given the array is searched as we cut the collection in half for each operation. This is oftentimes faster than a linear search.

public static int bSearch(int key, int[] arr) { int low = 0; int high = arr.length-1; while (low <= high) { int mid = (low + high) / 2; if (arr[mid] == x) return mid; // if key if found, return index if (arr[mid] < x) low = mid + 1; // If key greater, ignore left half else high = mid - 1; // If key is smaller, ignore right half } return -1;} //an iterative binary search algorithm for an int arraypublic static int bSearch(int low, int high, int key, int[] arr) { if (low <= high) { int mid = (low + high) / 2; if (arr[mid] == x) return mid; // if key if found, return index if (arr[mid] < x) return bSearch(mid + 1, high, key, arr); // If key greater, ignore left half else return bSearch(low, mid - 1, key, arr); // If key is smaller, ignore right half } return -1;} //an recursive binary search algorithm for an int array